Background
The modern world is built on graphs—from flight networks and navigation systems to the vast web of social connections. As these real-world graphs swell to include millions of vertices, finding optimal paths becomes a computational bottleneck. While sequential supercomputer implementations perform well, their hardware is prohibitively expensive. This project demonstrates how leveraging the power of General-Purpose Graphics Processing Units (GPGPU) can deliver massive performance improvements for fundamental graph pathfinding algorithms.
The Parallel Engine: The CUDA Programming Model
The key to unlocking performance on a GPU is Nvidia’s CUDA programming model. CUDA allows us to distribute a massive workload across the GPU’s thousands of cores using a software environment that supports C/C++.
The model organizes work using three core abstractions:
- Grids: The complete distributed workload.
- Blocks: Subdivisions of the grid.
- Threads: The fundamental unit of execution, where each thread is assigned a task.
The GPU hardware follows a Single-Instruction, Multiple-Thread (SIMT) architecture, similar to SIMD, meaning all threads execute the same instruction set but on different data in parallel. The main challenge in GPU programming is effectively mapping an irregular problem, like graph traversal, onto this highly restrictive, yet massively parallel, hardware.
Representing Massive Graphs for GPU Performance
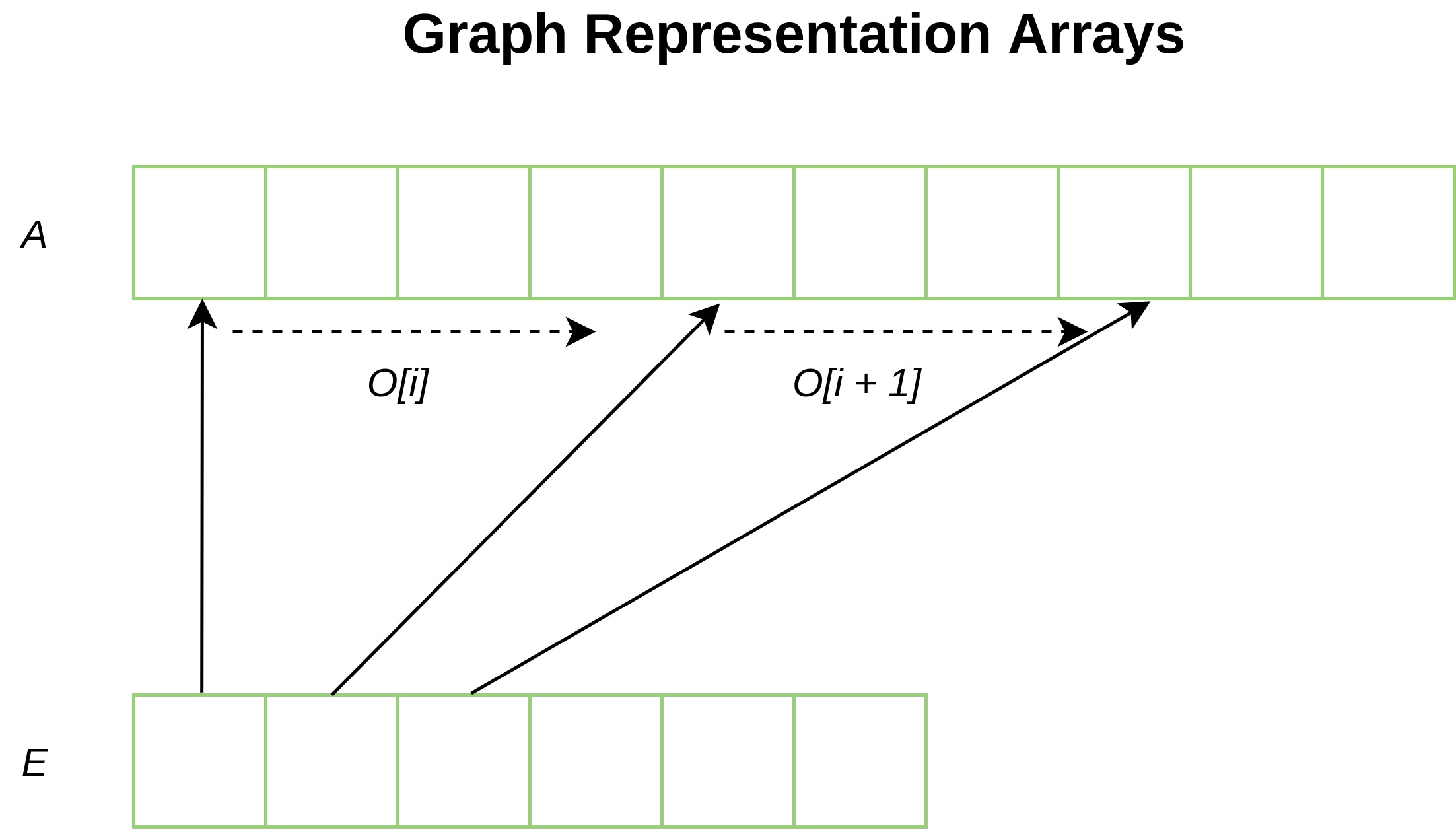
For optimal GPU processing, the choice of data structure is crucial. I opted for an Adjacency List due to its efficient space complexity, $O(V+E)$, where $V$ is the number of vertices and $E$ is the number of edges.
To facilitate efficient, contiguous GPU memory access, this list, $A$, is stored along with two essential auxiliary arrays:
- $E$: Holds all the offsets for each vertex.
- $O$: Holds the outdegree for a vertex $v$, meaning the children are located at $A[v]$ to $A[v+O[v]]$.
Case Study 1: Breadth-First Search (BFS) Parallelization
Breadth-First Search (BFS), defined on an undirected, unweighted graph $G(V,E)$, finds the minimum distance from a source vertex $S$ to every other vertex.
The serial approach uses a queue to ensure level-wise progression, which guarantees the shortest path is found. This sequential implementation has a time complexity of $O(V+E)$.
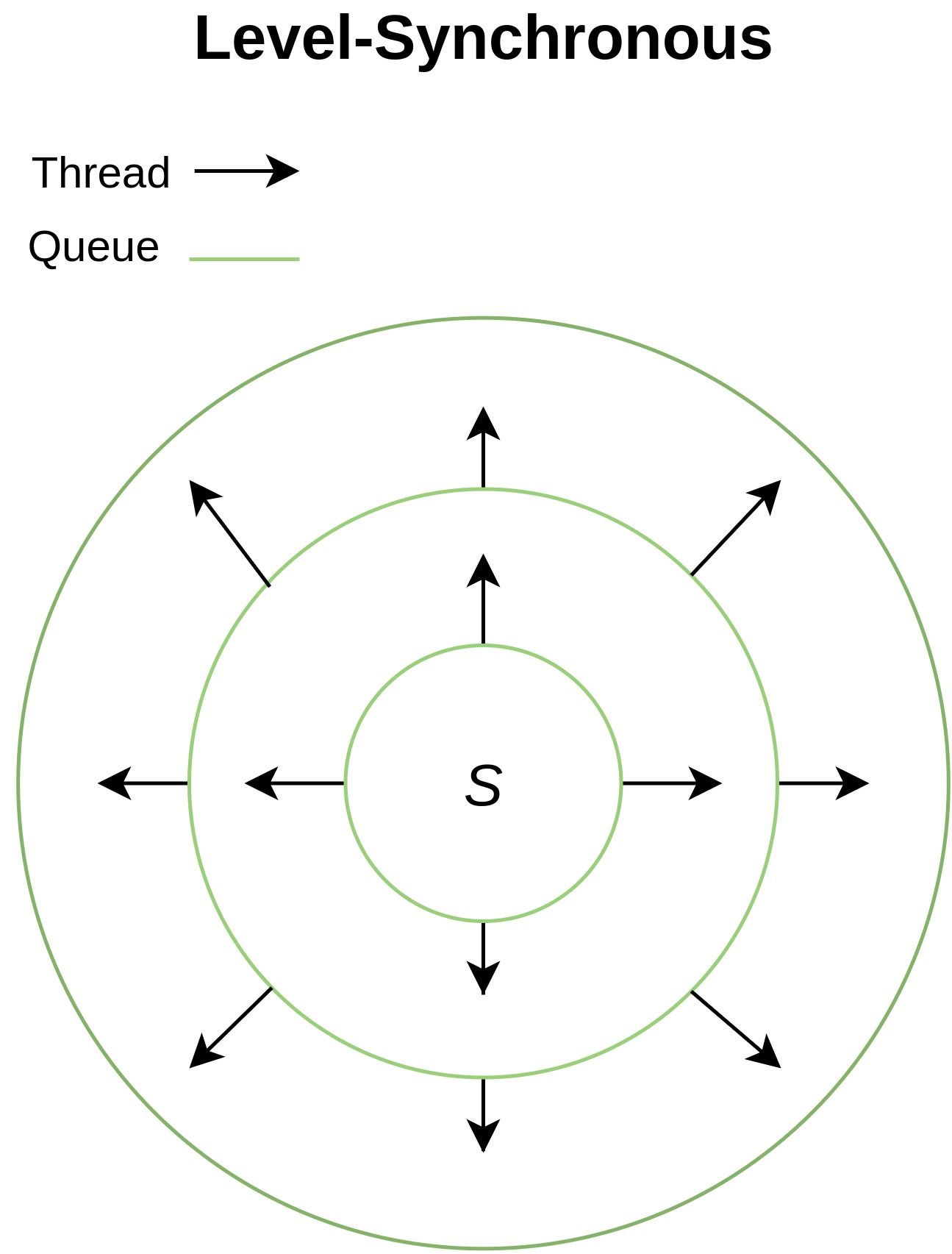
The Challenge of Level Synchronization
In a parallel BFS implementation, the only viable traversal method is level-synchronous. This requires distributing each vertex in the current queue level to a thread to explore its neighbors in parallel.
This method creates several performance bottlenecks:
- Kernel Launch Overhead: Since the algorithm proceeds level-by-level, the CUDA kernel must be launched for each new level, incurring the cost of data transfer latency between the CPU and GPU.
- Race Conditions: All threads need to update the same global queue for the next level, which can lead to data inconsistencies and conflicts.
- Memory Irregularity: Highly irregular access to global memory, common in sparse graphs with varying outdegrees, slows down performance.
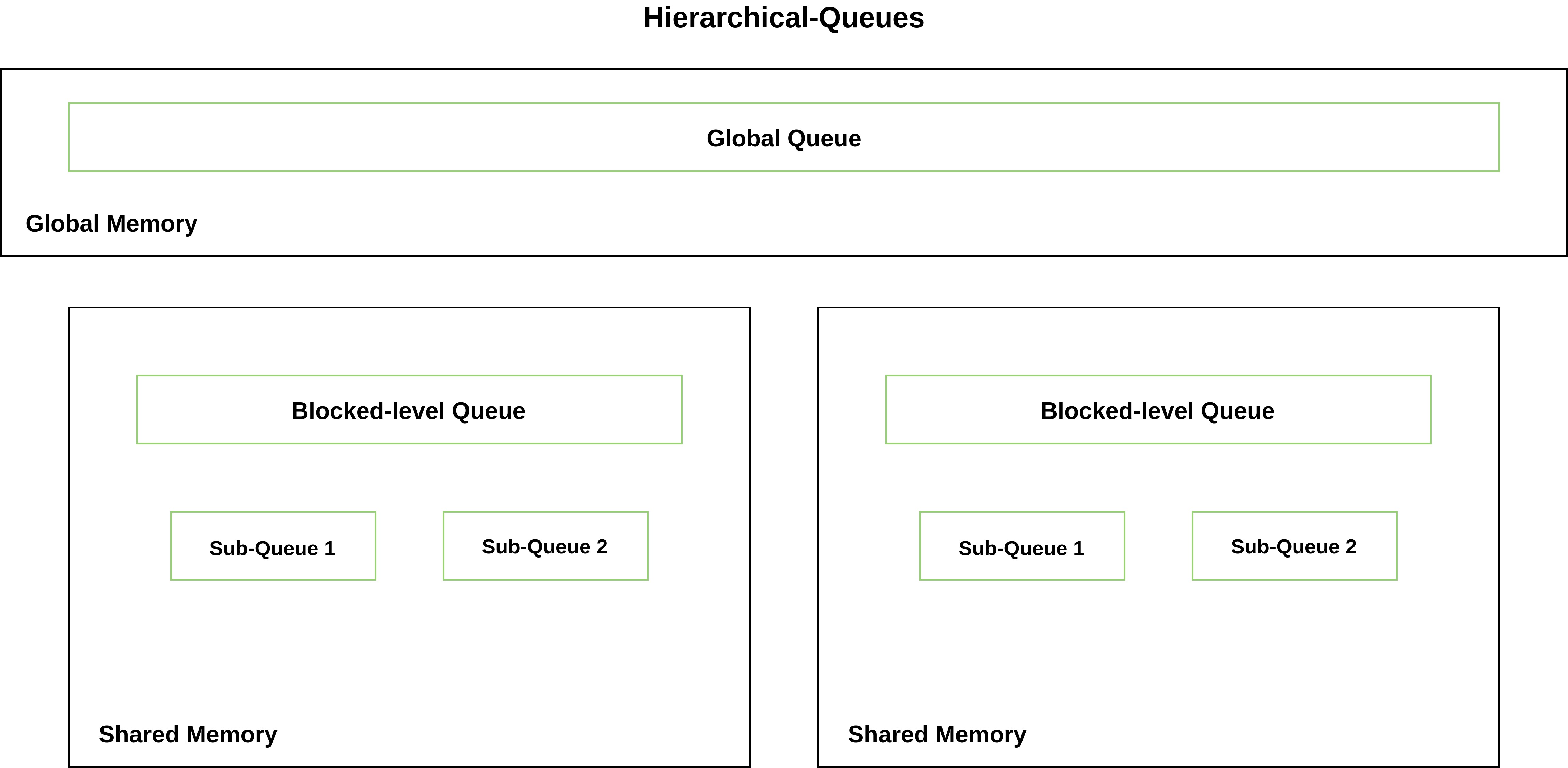
Solutions: Blocked and Hierarchical Queues
To mitigate race conditions and optimize memory access, I explored using the fast on-chip L2 Shared Memory available to each thread block.
- Blocked Queue Approach (GPU-B): Shared memory is used to maintain a block-level queue. Threads write to this queue first, and only when the block-level queue is full, or the block finishes exploration, is the data coalesced and written to the global queue.
- Hierarchical Queue Approach (GPU-H): This adds an additional level of specialization for warps. Threads are mapped to sub-queues within shared memory, further reducing collisions before writing directly to the global queue when the sub-queue fills up.
The Performance Gains
The table below shows the speedup achieved against the CPU execution using real-world sparse road graphs from the DIMACS shortest path datasets.
| G | V | E | CPU | GPU-N | GPU-B | GPU-H |
|---|---|---|---|---|---|---|
| New York | 264,346 | 733,846 | 29.9261 ms | $1.21times$ | $0.98times$ | $0.92times$ |
| California | 1,890,815 | 4,657,742 | 237.658 ms | $2.62times$ | $2.38times$ | $2.10times$ |
| Western USA | 6,262,104 | 15,248,146 | 857.753 ms | $4.38times$ | $4.09times$ | $3.97times$ |
| Central USA | 14,081,816 | 34,292,496 | 2625.37 ms | $mathbf{6.52times}$ | $6.11times$ | $6.15times$ |
| Whole USA | 23,947,347 | 58,333,344 | 3400.58 ms | $5.80times$ | $5.35times$ | $5.30times$ |
The results clearly demonstrate the power of GPGPU processing, achieving a peak speedup of $6.52times$ on the Central USA road network. Counterintuitively, the Naive Parallel Approach (GPU-N) often outperformed the shared memory approaches (GPU-B and GPU-H), possibly because the overhead of managing the block and warp queues outweighed the reduction in global memory contention for these graphs. The additional write operations and thread divergence also contributed to the performance deterioration of 6-8% in shared memory approaches compared to the naive BFS.
Case Study 2: Single-Source Shortest Path (SSSP)
Single-Source Shortest Path (SSSP) extends BFS to weighted graphs $G(V,E,W)$, finding the path with the minimum total weight from a source vertex $S$ to all others.
The classic serial Dijkstra’s Algorithm typically uses a priority queue to efficiently extract the minimum weighted edge. To avoid the parallelization complexity and $O(log n)$ overhead of a binary heap, the CPU implementation here avoids the priority queue and instead sorts the queue array at each iteration using a hybrid approach (Intro sort), resulting in a running time of $O(VE+Vlog V)$.
Parallel SSSP Adaptation
The Parallel SSSP approach closely mirrors the Parallel BFS. Since all vertices in the current level are processed in parallel, there’s no need for sorting or minimum extraction. The parallelization focuses on exploring neighbors and ensuring that distance updates are reflected when a shorter path to an already visited vertex is found. This was implemented using the Hierarchical-queue approach.
Lessons Learned: Pitfalls of GPU Optimization
Optimizing graph algorithms on the GPU is an exercise in managing highly irregular and memory-bound workloads. Not every standard GPU optimization technique translated into a performance gain. Here are the crucial lessons learned from what didn’t work:
1. Atomic Operations: The Cost of Synchronization
To ensure consistency in updating the global and local queues, we can use CUDA’s Atomic Operations. These functions provide exclusive access to a memory location, preventing threads from overwriting each other.
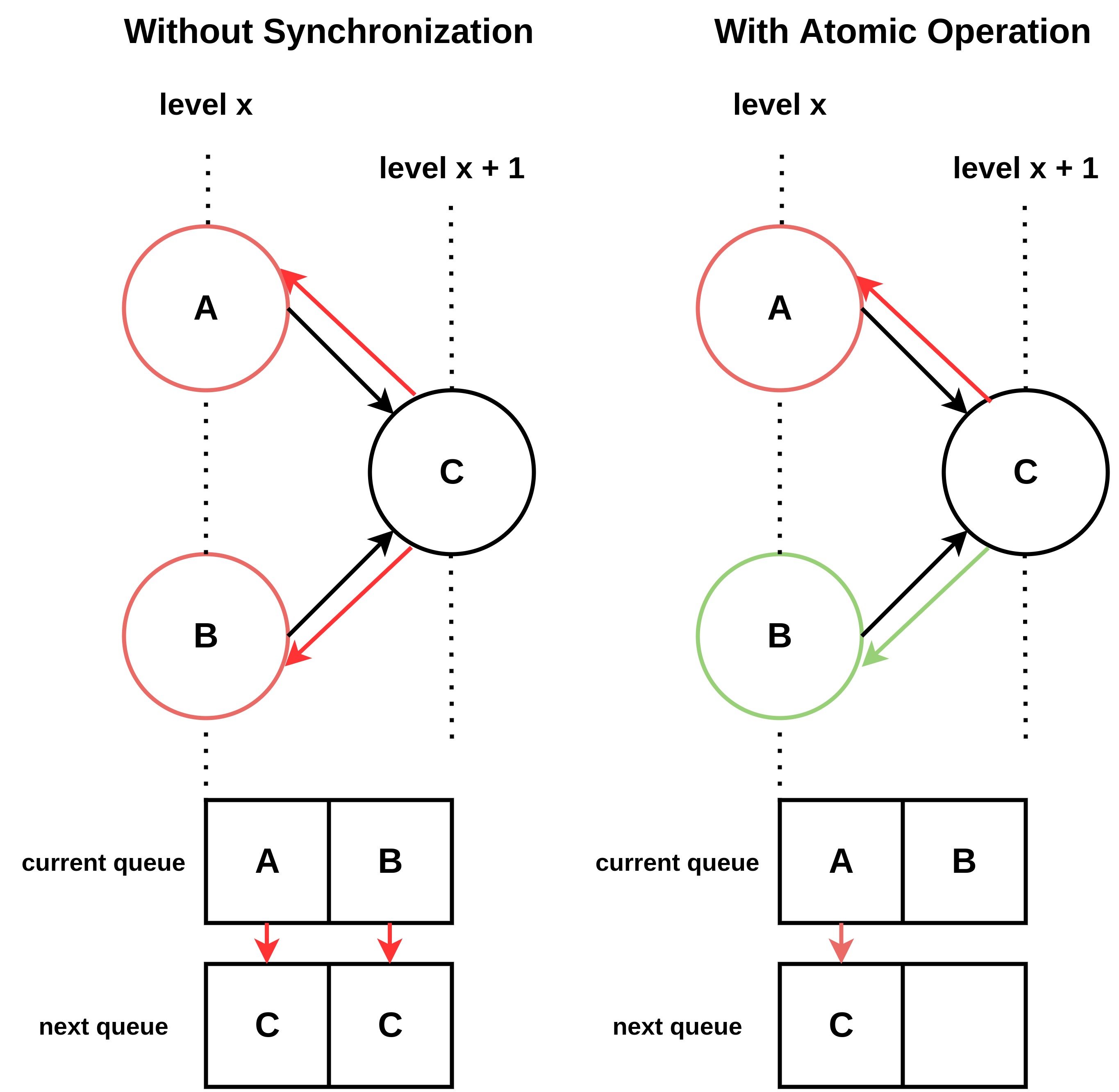
While atomically guaranteed to be correct, this approach forces threads into a serialized queue waiting line. The performance hit from this serialization often outweighs the benefit of concurrency, negatively impacting the overall execution time.
2. Shared Memory: Balancing Complexity and Contention
The use of fast, on-chip Shared Memory was explored to reduce global memory contention via Blocked and Hierarchical queue approaches.
-
Hierarchical Queue Design: My design for the Hierarchical Queue involved creating 32 queues of length 4, which perfectly matched the 32 banks in my GPU’s shared memory. For GPUs with Compute Capability (CC) 6.1, bank conflicts are eliminated at the warp level, even when multiple threads from the same warp map to the same bank, allowing for parallel access.
-
Performance Deterioration: Although this shared memory architecture reduces collisions, the overall performance of these approaches deteriorated by 6–8% compared to the Naive BFS implementation. The key reason is simplicity: the naive implementation has less thread divergence since each thread performs a simple check (is_visited?) before writing directly to global memory. The shared memory approaches, conversely, involve at least two writes: first to the lower shared queues, and then to the global queue.

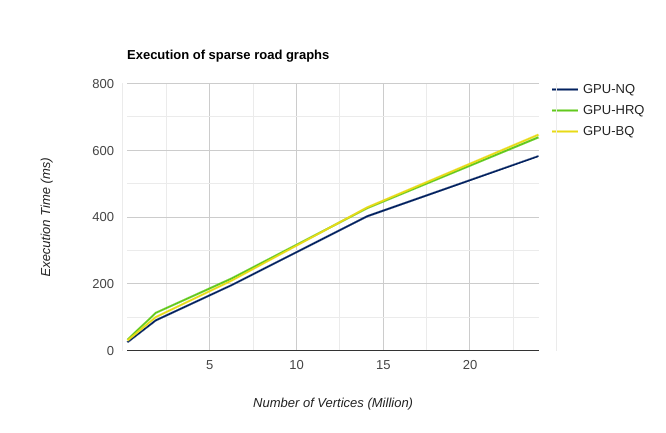
The graphs above, calculated on regular or near-regular graphs with an average outdegree between 2–3, show execution time being directly proportional to the number of vertices.
- Performance by Graph Type: The Hierarchical Queue generally performs better on graphs exhibiting a higher clustering coefficient. However, for smaller graphs, although both the Blocked and Hierarchical approaches have similar thread divergence during exploration, the Hierarchical Queue proved slower. This slowdown is attributed to the increased time and calculation required to map the 2D shared queue addresses into 1D global queue addresses when flushing data to global memory.
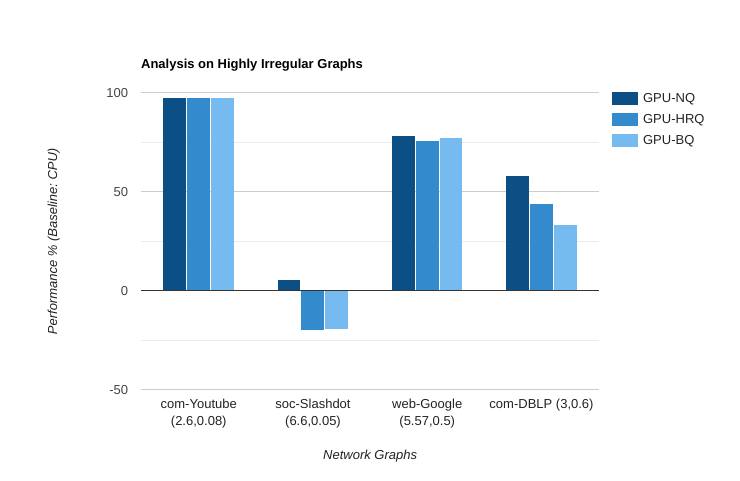
- Network Graph Considerations: The bar graph above was calculated using Network Graphs (Google, YouTube, etc.) characterized by varying clustering coefficients and unevenly distributed outdegrees. This high variance in outdegree — common in graphs where each vertex represents a user and their connections—significantly reduces performance. For such irregular graphs, an approach suggested by [D1] might be more effective.
3. Kernel Launch and Dynamic Parallelism
The level-synchronous nature of both BFS and SSSP mandates inter-level synchronization.
- Dynamic Parallelism (DP): I attempted to use CUDA’s DP—calling a kernel recursively from within the GPU—to move the outer loop logic onto the GPU and avoid the latency of repeated CPU-GPU data transfers.
- The Synchronization Wall: This approach hit a fundamental barrier: it requires grid synchronization to ensure all blocks at the current level are complete before launching the next. Unfortunately, the CUDA Cooperative Groups API does not permit the usage of DP with grid synchronization, leaving no straightforward workaround.
- Overhead: Even moving the outer loop to a CPU-launched kernel failed to yield significant speedup, suggesting the kernel launch overhead was comparable to the transfer latency itself.
4. Read-Only Caches: Lack of Locality
I investigated using CUDA’s aggressively cached Texture Memory (L2) for read-only graph arrays, such as the offsets. Texture memory excels when data exhibits spatial locality—meaning nearby threads read nearby addresses.
However, the irregular access patterns in pathfinding on large, sparse graphs do not offer the required spatial locality. Attempting to use this cache actually decreased performance by $11%$ in some cases, and even doubled execution times in others, likely due to a high rate of cache misses.
5. Prefix-Sum: Computational Trade-off
Another technique to avoid atomic operations is using Prefix-Sum (or parallel scan). This calculates the exact global queue offset for each thread based on the prefix-sum of their outdegrees.
While the Thrust library offers parallel implementations, this method requires computing a prefix-sum for the current queue at every outer loop iteration. The trade-off here is computational: does the cost of performing a parallel prefix-sum at each level outweigh the benefit of avoiding serialized atomic operations? This avenue was not fully explored but remains a high-level design question for graph parallelism.
Alternative Algorithms: Why They Were Not Prioritized
While BFS and SSSP were the core focus, we considered the feasibility of applying GPGPU to other common graph algorithms.
Depth-First Search (DFS)
DFS is inherently asynchronous, continuing the search from a single vertex until all its children are “relaxed”. This contrasts sharply with the level-synchronous nature of parallel BFS.
- Low GPU Utilization: Since the outdegrees are often not “unreasonably large,” DFS would make multiple calls with only a few threads launched per vertex. Unlike BFS, which operates on large queues at each level, DFS would fail to utilize the GPU’s full parallel capability, as GPUs excel with heavier, uniform loads.
- Parallel Stack Difficulty: DFS relies on backtracking, which requires a Stack data structure. Parallelizing a stack is complex because both insertion and extraction must occur at the same end, making simultaneous thread access difficult to manage.
A* Search
A* Search is essentially an expansion of SSSP that uses heuristics to guide the search, making it goal-directed.
- Heuristic Data Limitation: Implementing A* was impractical for the road network graphs used, as the datasets did not provide the necessary heuristic values for each vertex. Heuristics typically require a target vertex to approximate distances. While one could apply a parallel SSSP from the target to all vertices to obtain the heuristics, this is not an optimal real-world solution.
- Grid Structure Inefficiency: A* is highly effective in grid-like structures (e.g., mazes), where heuristics (like Manhattan or Euclidean distance) can be computed at runtime. However, even considering diagonal paths, parallelizing this results in launching a maximum of 8 threads per cell. Given that GPUs perform best with heavier loads, this degree of fine-grained parallelism is better suited for CPU cores and was deemed outside the project’s scope.
Computation Environment
All experimental computations were performed on the following local machine specifications:
| Component | Specification |
|---|---|
| CPU | Intel i5-7300HQ @ 2.50GHz (4 cores) |
| CPU RAM | 8 GB |
| GPU | Nvidia GeForce GTX 1050 mobile |
| GPU Clock | 1.49GHz |
| GPU RAM | 4 GB @ 3.5GHz |
| CUDA Cores | 640 |
Closure
This project successfully demonstrated that leveraging GPGPU usage can achieve substantial performance gains in Graph Algorithms. We established performance gaps between different parallel approaches (Naive, Blocked, Hierarchical) and provided insights into pre-existing optimization challenges.
While optimizing graph algorithms remains inherently difficult due to the irregular and uncertain nature of the graph structure, we obtained substantially great speed-ups. With further fine-tuning and algorithm-specific adjustments, these performance gains could likely be marginally increased.